Archive
Inferences for Gamma Sampling Problem
In the previous post, I considered the problem of modeling lengths of cell phone calls. Here we focus on several types of inferences and predictions that might be of interest.
Following the general computing strategy described in Chapter 5 of BCWR, I first transform the gamma parameters (alpha, beta) to (theta1 = log alpha, theta2 = log mu= log (alpha beta)). The function gamma.sampling.post computes the posterior of (theta1, theta2). The function mycontour draws a contour plot and the function simcontour simulates from this grid. The figure shows the contour plot with the simulated draws placed on top.
> y=c(12.2,.9,.8,5.3,2,1.2,1.2,1,.3,1.8,3.1,2.8)
> library(LearnBayes)
> gamma.sampling.post=function(theta,data)
+ {
+ a=exp(theta[,1])
+ mu=exp(theta[,2])
+ n=length(data)
+ val=0*a
+ for (i in 1:n) val=val+dgamma(data[i],shape=a,scale=mu/a,log=TRUE)
+ return(val-log(a)+log(a)+log(mu))
+ }
> mycontour(gamma.sampling.post,c(-1.5,1.5,0,3),y)
> title(main=”POSTERIOR OF (LOG ALPHA, LOG MU)”,xlab=”log alpha”,
+ ylab=”log mu”)
> s=simcontour(gamma.sampling.post,c(-1.5,1.5,0,3),y,1000)
> points(s$x,s$y)
Suppose we are interested in the mean length of cell phone calls mu. In particular, what is the probability that the mean length exceeds 4 minutes? The figure displays a density estimate of the simulated draws of mu, and I have labeled the desired probability.
> mu=exp(s$y)
> alpha=exp(s$x)
> beta=mu/alpha
> plot(density(mu),main=”POSTERIOR OF MEAN LENGTH”,xlab=”mu”,lwd=3)
> lines(c(4,4),c(0,ss$y[135]),lwd=3)
> text(8,.15,”P(MU > 4) = 0.178″)
> arrows(7,.1,4.5,.05,lwd=2)

Next, suppose we are interested in the predictive distribution of the length of a single cell phone call. Since we have already collected simulated draws from the posterior of (alpha, beta), it just takes one additional command to simulate the predictive distribution of y* (using the function rgamma). I have displayed a density estimate of the predictive density.
Note that the probability the mean call length exceeds 4 minutes is 0.178; the probability a future call exceeds 4 minutes is 0.263
> ys=rgamma(1000,shape=alpha,scale=beta)
> plot(density(ys),xlab=”CALL LENGTH”, lwd=3, main=”POSTERIOR PREDICTIVE DENSITY”)
> mean(ys>4)
[1] 0.263

Last, suppose you plan on making 20 calls next month and you’re interested in the total amount of time used. By use of a loop, we simulate 20 draws from the predictive distribution — the variable ysum contains 1000 realizations of the total.
> ysum=rep(0,1000)
> for (j in 1:20) ysum=ysum+rgamma(1000,shape=alpha,scale=beta)
> hist(ysum, main=”PREDICTIVE DISTRIBUTION OF LENGTH OF 20 CALLS”)
Modeling Cell Phone Call Durations with a Gamma Density
Suppose we observe a sample y1, …, yn from a gamma(alpha, beta) density where the sampling density is proportional to y^{alpha-1} exp(-y/beta), and we assign a uniform prior on (alpha, beta).
As an example, suppose we wish to fit a gamma density to the durations (in minutes) of a group of cell phone calls.
12.2 0.9 0.8 5.3 2.0 1.2 1.2 1.0 0.3 1.8 3.1 2.8
Here is the R function that computes the log posterior of the density:
gamma.sampling.post1=function(theta,data)
{
a=theta[,1]
b=theta[,2]
n=length(data)
val=0*a
for (i in 1:n) val=val+dgamma(data[i],shape=a,scale=b,log=TRUE)
return(val)
}
The first figure is a contour graph of the posterior density of (alpha, beta). (In R, beta is called the scale parameter.) Note the strong curvature in the posterior.
Note the strong curvature in the posterior.
Instead, suppose we consider the joint posterior of alpha and the “rate” parameter theta = 1/beta. Here is a contour plot of the posterior of (alpha, theta).
 This doesn’t display the strong curvature.
This doesn’t display the strong curvature.
Last, suppose you consider the joint posterior of alpha and the mean mu = alpha beta. The last figure displays the posterior of (alpha, mu). The moral here is that the choice of parameterization can be important when summarizing the posterior distribution. In the next chapter, we’ll suggest a rule of thumb for transforming parameters that makes it easier to summarize many posteriors.
The moral here is that the choice of parameterization can be important when summarizing the posterior distribution. In the next chapter, we’ll suggest a rule of thumb for transforming parameters that makes it easier to summarize many posteriors.
Fitting a Beta Sampling Model

To illustrate a “brute-force” method of summarizing a posterior, suppose that we observe a sample y1, …, yn from a beta distribution with parameters a and b. If we assign (a, b) a uniform prior, then the posterior density is given by
g(a, b | data) propto prod_{i=1}^n f(y_i; a, b),
where f(y; a, b) = 1/B(a, b) y^(a-1) (1-y)^(b-1) is the beta density. As an example, suppose we are given the following proportions of students who are “math proficient” on the Ohio Graduation Test for a random sample of 20 schools in Ohio.
y=c(0.955, 0.819, 0.472, 0.925, 0.780, 0.931, 0.945, 0.926, 0.852, 0.920, 0.885, 0.890, 0.789, 0.973, 0.831, 0.835, 0.884, 0.904, 0.900, 0.806)
Here is our method:
1. We write a short R function betasampling.post.R that computes the logarithm of the posterior density. Note that the built-in function dbeta is used — the log=TRUE option gives the logarithm of the beta density.
betasampling.post=function(theta,data)
{
a=theta[,1]
b=theta[,2]
n=length(data)
val=0*a
for (i in 1:n) val=val+dbeta(data[i],a,b,log=TRUE)
return(val)
}
2. Next, by trial and error, we find a rectangle (a_lo, a_hi, b_lo, b_hi) that contains the contour plot of the joint posterior (remember that the contours given in the function mycontour.R are located at 10%, 1%, and 0.1% of the height of the density at the mode.)
mycontour(betasampling.post,c(.001,35,.001,6),y)
title(main=”Posterior density of (a, b)”,xlab=”a”,ylab=”b”)
3. We then sample from the grid of values of (a, b) that is used in constructing the scatterplot.
s=simcontour(betasampling.post,c(.001,35,.001,6),y,1000)
4. Suppose we are interested in the marginal posterior densities of a and b. We find these by use of density estimates on the simulated draws of a and b.
par(mfrow=c(2,1))
plot(density(s$x),main=”POSTERIOR OF a”,xlab=”a”,lwd=3)
plot(density(s$y),main=”POSTERIOR OF b”,xlab=”b”,lwd=3)
Conditional means prior
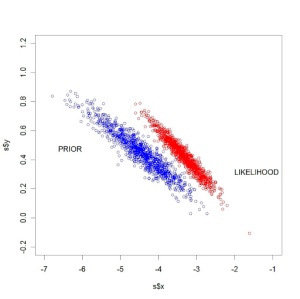
In an earlier post, we illustrated Bayesian fitting of a logistic model using a noninformative prior. Suppose instead that we have subjective beliefs about the regression vector. A convenient way of representing these beliefs is by use of a conditional means prior. We illustrate this for our math placement example.
First, we consider the probability p1 that a student in placement level 1 receives an A in the class. Our best guess at p1 is 0.05 and this belief is worth 200 observations — we match this info to a beta(200*0.05, 200*0.95) prior. Next, we consider the probability p5 that a student in level 5 gets an A — our guess at this probability is 0.15 and this guess is worth 200 observations. We match this belief to a beta(200*0.15, 200*0.85) prior. Assuming that our beliefs about p1 and p5 are independent, the joint prior on (p1, p5) is a product of beta densities. Transforming back to the (beta0, beta1) scale, one can show that the prior on beta is given by
g(beta) = p1^a1 (1-p1)^b1 p5^a2 (1-p5)^b2
(Note that the conditional means prior translates to the same functional form as the likelihood where the beta parameters a1, b1, a2, b2 play the role of “prior data”.)
The below figure displays (in red) a sample from the likelihood and (in blue) a sample from the prior. Here we see some conflict between the prior beliefs and the data information about the parameter.
Using a Mixture of Conjugate Priors
One way to extend the use of conjugate priors is by the use of discrete mixtures. Here is a simple example. Suppose you have a coin that you believe may be fair or biased towards heads. If p represents the probability of flipping heads, then suppose your prior is
g(p) = 0.5 beta(p, 20, 20) + 0.5 beta(p, 30, 10)
Suppose that we flip the coin 30 and get 20 heads. It can be shown that the posterior density can also be represented by a mixture of beta distributions.
I have written a short R function pbetamix that computes the posterior distribution when a proportion has a prior that is a mixture of beta distributions.
The matrix bpar contains the beta parameters where each row gives the beta parameters for each component. The vector prob gives the prior probabilities of the components. The vector data contains the number of successes and failures. Here are the values of these components for the example.
> bpar=rbind(c(20,20),c(30,10))
> prob=c(.5,.5)
> data=c(20,10)
We use the function pbetamix with the inputs prob, bpar, and data. The output is the posterior probabilities of the components and the beta parameters of each component.
> pbetamix(prob,bpar,data)
$probs
[1] 0.3457597 0.6542403
$betapar
[,1] [,2]
[1,] 40 30
[2,] 50 20
The posterior density is
g(p | data) = 0.346 beta(p, 40, 30) + 0.654 beta(p, 50, 20)
We plot the prior and posterior densities
> plot(p,.5*dbeta(p,30,30)+.5*dbeta(p,30,10),type=”l”,ylim=c(0,5),col=”red”,lwd=2)
> lines(p,.346*dbeta(p,40,30)+.654*dbeta(p,50,20),lwd=2,col=”blue”)
> text(locator(n=1),”PRIOR”)
> text(locator(n=1),”POSTERIOR”)
Here the data (20 heads and 10 tails) is more supportive of the belief that the coin is biased and the posterior places more of its mass where p > .5.
Fitting a logistic model

Freshman students at BGSU take a mathematics placement test and a “placement score” is used to advise the student on the proper first mathematics course. For students taking a business calculus course, we record (1) his or her placement score and (2) his or her grade in the course. There are five possible placement levels that we code as 1, 2, 3, 4, 5. Let yi denote the number of students receiving A at placement level i. We suppose that yi is binomial(ni, pi), where pi is the probability a student at level i receives an A in the class. We let the probabilities satisfy the logistic model
logit(pi) = beta0 + beta1 i.
Assuming a uniform prior for beta = (beta0, beta1), the posterior distribution is proportional to
g(beta) = product pi^yi (1-pi)^(ni-yi).
The definition of the log posterior of beta is defined in the R function logisticpost.R.
We illustrate a “brute force” method of fitting this model.
1. We first read in the data — we create three vectors y, n, and level. The matrix
data has columns level, n, and y.
> y=c(2,15,29,39,15)
> n=c(34,170,283,243,59)
> level=1:5
> data=cbind(level,n,y)
> data
level n y
[1,] 1 34 2
[2,] 2 170 15
[3,] 3 283 29
[4,] 4 243 39
[5,] 5 59 15
2. We illustrate the usual MLE fit using the R function glm. The MLE will be helpful in finding where the posterior is located.
> response=cbind(y,n-y)
> glm(response~level,family=binomial)
Coefficients:
(Intercept) level
-3.328 0.423
3. After some trial and error, we find a rectangle where the posterior is concentrated. The function mycontour is used to draw a contour plot.
> mycontour(logisticpost,c(-5,-1.5,-.2,1),data)
4. The function simcontour is used to simulate draws from the posterior computed on this grid. We plot the simulated draws on top of the scatterplot.
> s=simcontour(logisticpost,c(-5,-1.5,-.2,1),data,1000)
> points(s$x,s$y)
> title(xlab=”BETA0″,ylab=”BETA1″)
Example of Normal Inference

To illustrate inference about a normal mean, suppose we are interested in learning about the mean math ACT score for the students who are currently taking business calculus. I take a random sample of 20 students and put the values in the R vector y.
> y=sample(placedata$ACT,size=20)
> y
[1] 20 22 22 19 27 17 21 21 20 19 17 18 20 21 20 17 18 21 17 20
I compute some summary statistics.
> ybar=mean(y)
> S=sum((y-ybar)^2)
> n=length(y)
The definition of the log posterior of (mean, variance) with a noninformative prior is stored in the R function normchi2post. I construct a contour plot of this density by use of the mycontour function.
> mycontour(normchi2post, c(17,23,1.8,20),y)
> title(xlab=”MEAN”,ylab=”VARIANCE”)
To simulate draws of (mean, variance), I first simulate 1000 draws of the variance parameter from the scale times inverse chi-square density, and then simulate draws of the mean parameter. I plot the simulated draws on top of the contour density
> sigma2 = S/rchisq(1000, n – 1)
> mu = rnorm(1000, mean = ybar, sd = sqrt(sigma2)/sqrt(n))
> points(mu,sigma2)
Suppose we are interested in inferences about the 90th percentile of the population curve that is given by Q = mu + sigma z, where z is the 90th percentile of the standard normal. One can obtain a simulated sample from this posterior by simply computing Q on the simulated draws of (mu, variance).
> Q=mu+sqrt(sigma2)*qnorm(.90)
I draw the posterior density of Q by use of a density estimate on the simulated sample.
> plot(density(Q),main=”POSTERIOR FOR 90TH PERCENTILE”,lwd=3)
Evolution of statistical thought
One of you asked for some Bayesian/frequentist humor. This cartoon describes the historical evolution of statistical thinking. (This was taken from Mike West’s website.)
Any R problems?
Here’s your opportunity to post any problems you’re having using R. I’ll try to respond to each problem.
Test of hypothesis that coin is fair

In Section 3.5, I describe a Bayesian test of the hypothesis H that a proportion is equal to 0.5. The R function pbetat.R (in the LearnBayes package) computes the posterior probability of H assuming a beta prior on the alternative hypothesis. We illustrate how the posterior probability depends on the beta parameter a.
Here’s a quick way of constructing Figure 3.5 (page 52) using the curve function.
First we revise the function pbetat to accept a matrix argument for the beta parameters where each row of the matrix corresponds to a pair (a, b). The new function is called pbetat.v. Next, we write a short function best that computes the posterior probability of H for our example (5 successes and 15 failures) for a vector of values of log a. (We are assuming a symmetric beta(a, a) prior on the alternative hypothesis.)
best=function(loga)
{p0=.5; prob=.5
data=c(5,15)
AB=exp(cbind(loga,loga))
s=pbetat.v(p0,prob,AB,data)
return(s$post)}
To generate the figure, we can use the curve function.
curve(best,from=-4,to=5,xlab=”log a”,ylab=”Prob(coin is fair)”,lwd=3)
We see that for all values of the beta parameter a, the posterior probability of the hypothesis exceeds 0.2.


