Learning about a correlation – part II

Earlier we considered the problem of learning about a correlation and illustrated a normal approximation.  Here we illustrate rejection sampling to obtain a simulated sample from the exact posterior.

The main task is to find a suitable proposal density p.  We’ll let p be a t density with mean , variance and small degrees of freedom .

How to choose the parameters?  First, since the posterior is approximately N(0.50, 0.009), we’ll let and .  Also, we’ll choose the degrees of freedom .  (It is a good strategy to have a proposal density with “flat” tails which we achieve by choosing a small number of degrees of freedom.)

Next, we have to find the constant so that for all .  On the log scale, we want to find such that

.

I compute a small function that computes :

dfunction=function(rho,data)

cor.sampling(rho,data)-dmt(rho,.5,.009,4,log=TRUE)

dfunction=function(rho,data)
cor.sampling(rho,data)-dmt(rho,.5,.009,4,log=TRUE)

I plot this function over the range of values of from -1 to 1 — I find that

log c = -42.9927.

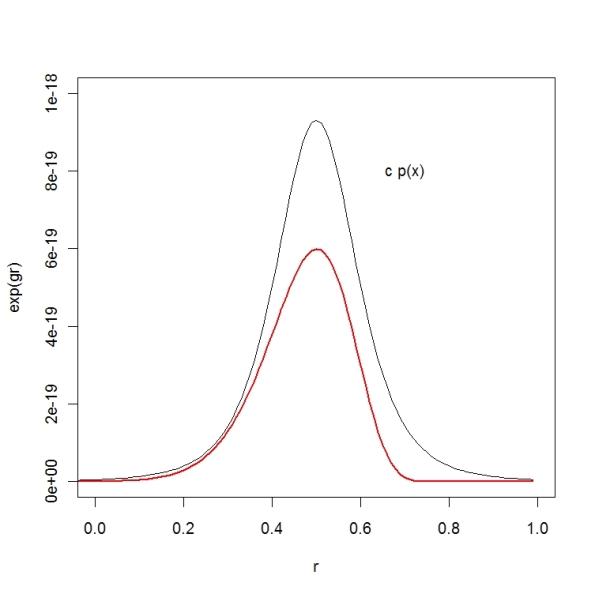
To see if I have found a suitable covering function, I plot the exact posterior and the covering density .  It looks pretty good.

Now we can implement rejection sampling.   We can use a LearnBayes function rejectsampling.

R=rejectsampling(cor.sampling,list(m=.5,var=.009,df=4), dmax=-42.9927,10000,dz)

The inputs are (1) the exact log posterior function, (2) the parameters of the t proposal density (mean, variance, df), (3) the value of log c, (4) the number of values we propose, and (5) the data used in the log posterior.

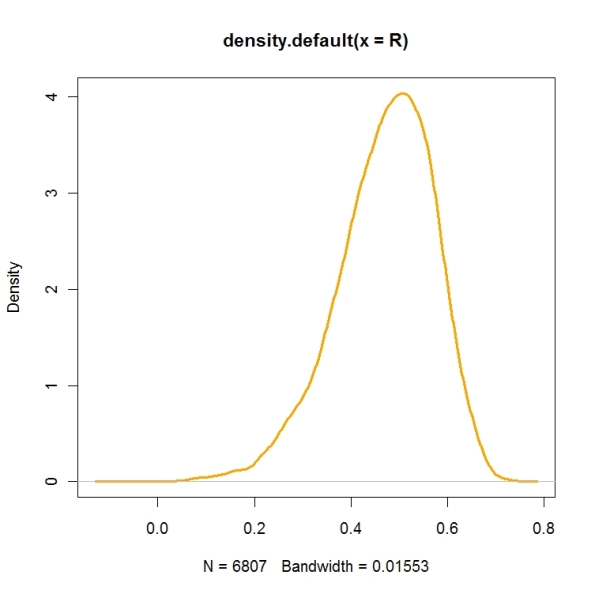
Here is a density estimate of the simulated draws we get — this is very close to the exact posterior density.

plot(density(R),col=”orange”,lwd=3)